So What Is This, Anyway?
The Dragon Curve is a simple fractal shape.
Fractals are characterized by being symmetrical across scale, meaning their shapes repeat at different sizes.
Many objects in nature have fractal characteristics: trees, blood vessels, and mountains, for example.
The Dragon Curve fractal is made using a very simple set of rules:
- Start with a line going down.
- From the end point, rotate the shape 90° counter-clockwise.
- Repeat the process, starting from the new end point, and rotating 90°
counter-clockwise.
- With successive iterations, patterns begin to emerge.
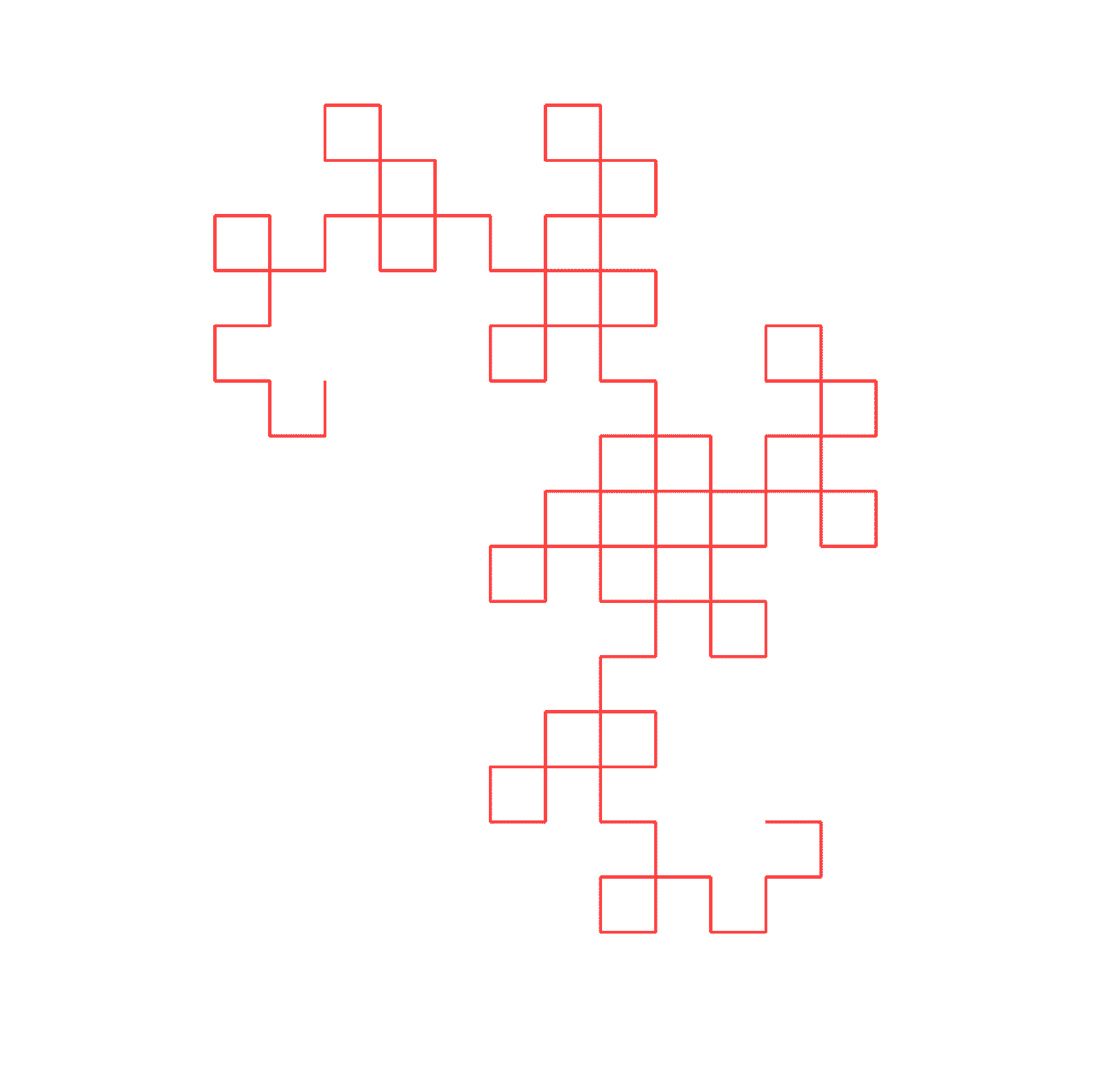
- The pattern grows exponentially, doubling in size with each iteration.
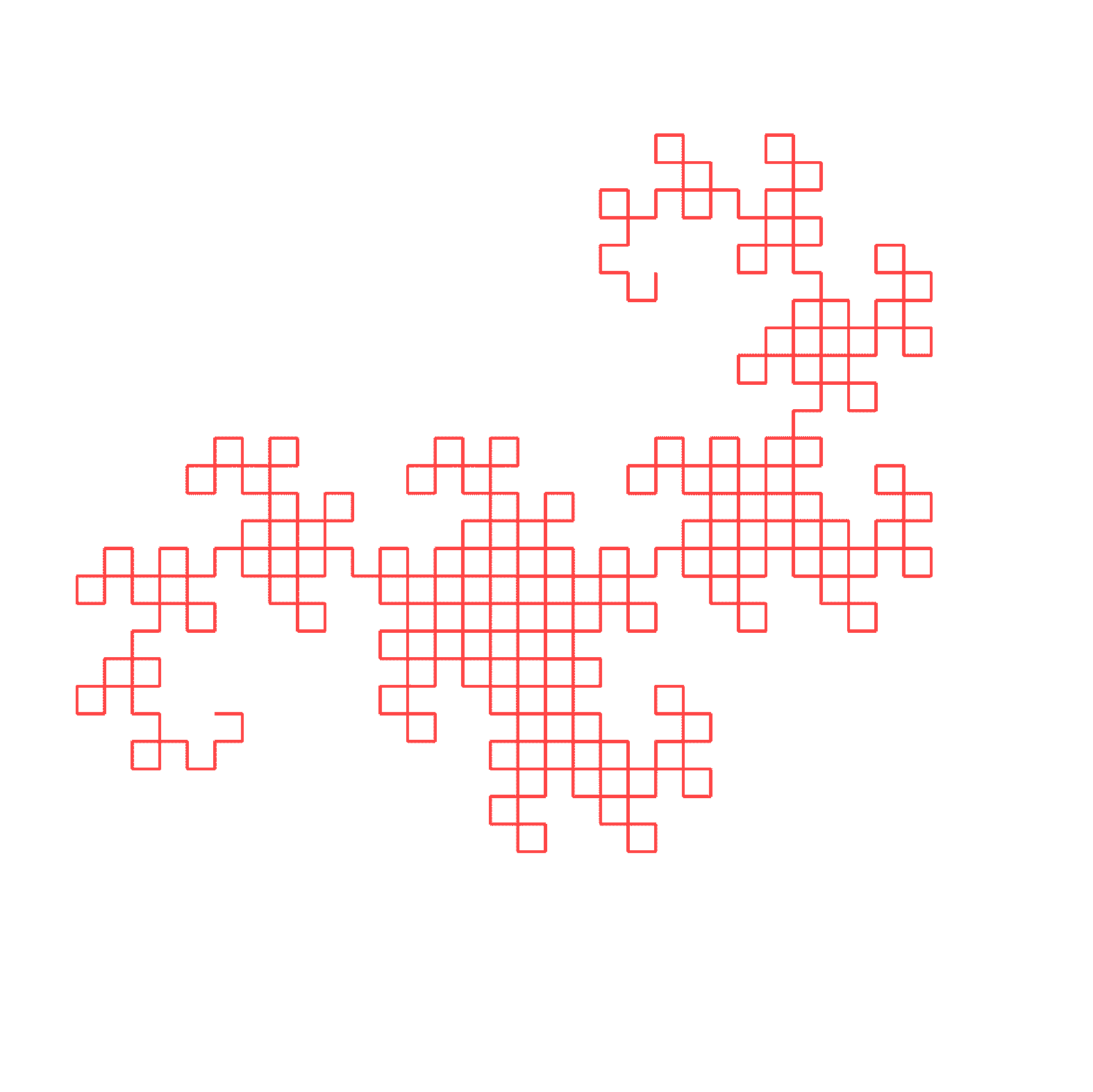

- The first iteration had just two lines, but the eighteenth iteration has over a
quarter-million lines. Seen from a distance, individual lines blend together into a solid
color.

Dragon Curves were famously used in Michael Crichton's novel Jurassic Park, where mathematician Dr. Ian Malcolm uses them to illustrate the chaos inherent in the park's design.

2015 paperback, p. 199.
A Dragon Curve uses very simple rules, but from those simple rules, elaborate, unforseen patterns emerge.
In the same way, the rules governing Jurassic Park and its dinosaurs seem simple and foolproof to the park's designers, but lead to unpredictable, catastrophic results.
The Dragon Curve was programmed using Vanilla JS and the HTML5 Canvas element.
AS HOME DECOR
One unusual property of the Dragon Curve is that never overlaps itself. This means that a Dragon Curve can be used to tile a surface.
By creating four Dragon Curves of different colors, each rotated 90° from the previous one, I can create a Dragon Curve grid.
I then used Legos™ to tile my coffee table with a Dragon Curve pattern.
Click on photos to enlarge.
Using a modified version of my program, a Dragon Curve tile can be made for any size surface.
CREDITS
- Dragon Curve Drawing Function created by Nicholas Bernhard




